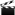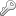Posted 16 November 2013 - 01:06 AM
Decided to stop off at Starbucks and finish my entry about mapping Rubik's cube algorithms, so I did, and here it is:
I’ll preface this very simply. I explore how it’s possible to leverage cognitive power to be able to solve a Rubik’s cube blindfolded, and I do it in part by conceptually mapping algorithms through the use of my own logical tool, which I call two-point theory. I’ll be very clear: This isn’t a tutorial on how to actually solve a Rubik’s cube blindfolded, although it could very well be used as a guide to approaching the task.
As anybody reading this probably already knows, Rubik’s cubes are solved by the application of algorithms, and the more algorithms you know, the faster and more efficiently you can solve them. To see the benefit with respect to memory, consider how this employs what’s known as “chunking.” With each algorithm functioning as a group comprised of specific turns, your brain operates through a sort of shorthand, which reduces the stress placed on memory from remembering the total number of turns, n, to n divided by t, the mean number of turns per algorithm. One example illustrating the same benefit is dictionary-based algorithms, like those used in compression systems. By picking out pattern redundancies, a code can be created to represent segments of information. Of course, the code itself would take up some space, but as the information that’s being compressed increases, the benefit, in terms of compression, lies in the difference in space used.
Here’s a quick illustration. If you let s represent the space occupied before compression, then the benefit can be represented as s - (d+ c), where d is the space occupied by the dictionary, and c is the net amount of information remaining after compression. You can think of s as the total number of turns needed to solve a Rubik’s cube from a given position and c as the number of algorithms used (Notice how c is the equivalent of n/t, explained above.).
Now that’s all well and good, but let’s step away from the algorithms for a moment to discuss a logical tool that I think lends itself here quite nicely. I call the tool, or theory, the two-point theory, and basically it works by defining a spectrum, or segment, for the context of a subject, which in turn illustrates the limitations for the subject matter, much like a graph illustrates the possible inputs and outputs for a function. In other words, it works to demonstrate the range of something by defining spectral ends. In addition, depending upon the nature of the spectrum, it allows you to deduce a quality—or set of qualities—that a subject must posses. For example, if c is defined as a point resting somewhere along the segment AB, and all points within that segment possess a certain quality, q, then you can conclude that c must have quality q.
In concept it’s very simple. Now let’s apply it to our situation with the Rubik’s cube. For this we’ll have to map out, at least in concept, the spectral ends of algorithms as they converge to form a solved Rubik’s cube, and because I don’t have any fancy art program, I’ll have to make do with an array of generic arrows. I’ll label the spectrum AB, where A and B are the spectral ends. The letters with the “subscripts” represent algorithms.
End A:
A0 → A1 → A2 → A3 → A4 → A5 → A6 → A7 → (converges with solved)
B0 → B1 → B2 → B3 → B4 → B5 → B6 → B7 → (converges with solved)
C0 → C1 → C2 → C3 → C4 → C5 → C6 → C7 → solved
D0 → D1 → D2 → D3 → D4 → D5 → D6 → D7 → (converges with solved)
E0 → E1 → E2 → E3 → E4 → E5 → E6 → E7 → (converges with solved)
height and length (independent) = [1, ∞)
End B:
A0 → (converges with B1)
B0 → B1 → (converges with solved)
C0 → C1 → solved
D0 → D1 → (converges with solved)
E0 → (converges with D1)
height and length (dependent) = [1, ∞)
Originally I used diagonal arrows, but the website rejected the icons.
You’ll just have to use your imagination and pretend that I used the formal notation with subscripts in decrements of n, n - 1, n - 2, ..., 2, 1, etc. I don’t know how to use subscripts, and the point’s just as clear without them. Also, the use of infinity, although in a formal context, is technically incorrect, but this has no logical bearing on the information the mapping provides, and it’s much simpler this way.
So how does this relate to our discussion about the Rubik’s cube? Well, if ends A and B cover all possible positions and progressions for a Rubik’s cube, then any position, a, could be defined as (A, a] ∪ [a, B), or, equivalently, A (less than or equal to) a (less than or equal to) B. But, you may ask, “What makes B’s value greater than A’s? Couldn’t it just as easily be the other way around?” Very astute, dear reader. Yes, it could. The order doesn’t matter; it’s all about relative position. Anyway, what this means is that a person attempting to solve a Rubik’s cube blindfolded must only—and I use that word loosely—be able to determine which algorithm to start with and then all subsequent algorithms that follow from that line. Moreover, unless the starting position results in a pattern that perfectly mirrors spectral end A, the algorithms used will involve some level of convergence, which means that the solver could find the solution with knowing even fewer algorithms. Put simply, the solver need only identify which algorithmic line to follow, and, of course, he or she could do that with their eyes open in the time allotted to survey the cube. One caveat, however, is that all outputs for the algorithms must be functionally based, meaning that each algorithm must be such that it provides only one output, which may or may not be unique with respect to other algorithms (just like a surjective function).
Well, I hope that demystifies the subject a little.