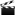Are those plastic storage containers food grade? BPA free? Not affected by the acid?
I don't really know, but the plastic tube is designed to hold the hydrogen rich water stick, which you put in your drinking water, and thus this stick itself is presumably food grade, so possibly its holding container might be also. But I don't know. I am not too concerned myself. You probably get more transdermal exposure to BPA when holding the handles of your PVC sports bag with sweaty hands.
The acid does not seem to affect the plastic tube as far as I can see, having used this plastic tube dozens of times.
- Might as well use up the malic acid if acceptable. Should we use 4 grams of it plus water to go into the storage container with the 1 magnesium rod?
Whatever you have handy will work fine: malic, citric or acetic.
I buy 100 grams of citric acid powder for 79 pence in the local Asian grocery shop across the road from me (it is used in cooking as a meat tenderizer and condiment), so that is a cheap option. If you use 3 grams of citric acid each time, it works out to 2.4 pence per bottle of hydrogen rich water.
And for around 40 pence you can buy 500 ml of distilled vinegar in a supermarket (you only need around 30 ml of vinegar each time, so that works out to 2.5 pence per bottle).
If you buy citric acid powder in bulk, I have seen prices of £20 for 5 kg, which would then work out at 1.2 pence per bottle.
The chemical reactions involved in creating hydrogen from the reaction with the magnesium rod are:
Magnesium + malic acid + —> hydrogen gas + magnesium malate
Mg + C4H6O5 —> H2 + MgC4H4O5
Magnesium + citric acid —> hydrogen gas + magnesium citrate
Mg + C6H8O7 —> H2 + MgC6H6O7
Magnesium + water —> hydrogen gas + magnesium hydroxide
Mg + H2O —> H2 + Mg(OH)2
If you do your molar mass calculations, you can work out that: each gram of citric acid reacting with the magnesium rod creates a volume of 125 ml of H2 gas (at 20ºC and normal atmospheric pressure). So 3 grams of citric acid will create a volume of 375 ml of H2.
And each gram of malic acid reacting with the magnesium rod creates a volume of 179 ml of H2 gas (at 20ºC and normal atmospheric pressure).
Note though that you also get some H2 gas being produced from the reaction between the magnesium rod and water, which takes place at the same time as the reaction between the magnesium rod and the acid.
When I use 3 grams of citric acid, I generate around 450 to 500 ml of H2 gas, so I think most of that H2 gas comes from the reaction with the acid, and some H2 comes from the reaction of magnesium with the water.
In terms of how much magnesium is used up from the reaction, 3 grams of citric acid will react with 127 mg of magnesium, by my molar mass calculations. That means that one 100 mm x 18 mm magnesium rod, which weighs 44 grams, will be able to make 346 bottles of hydrogen rich water, if you use 3 grams of citric acid each time. In fact it will be slightly less than this 346 figure, because as mentioned, magnesium also reacts with the water, which uses up some magnesium.
(If you let you bottle brew for 24 hours, I guess even though the acid may be used up within the first hour or two, magnesium's reaction with water will continue, and you will use up more magnesium compared to brewing for say just 1 or 2 hours.)
But let's say as a conservative estimate that one magnesium rod will last for 250 brews, then given each 100 mm x 18 mm magnesium rod costs around £2 on eBay, that means the magnesium cost per brew is 0.8 pence.
- Temperatures for the inner and outer waters?
- Brewing times?
- Bottle capacity?
These details are not yet settled, and are still being investigated. But if you glance through this thread from about page 10 onwards, you will find lots of discussion about these parameters.
The "test tube within a bottle" method I have been experimenting with is first detailed in this post on page 10, and then has been developed and discussed on subsequent pages with the very helpful ideas, insights and enthusiasm of @aconita, plus the pioneering original hydrogen rich water making method of @streamlover (see his video and method in this post).
But some guidelines for using the "test tube within a bottle" method might be these:
Reagents: around 3 grams of citric acid or malic acid, plus one magnesium rod.
Temperature: room temp (20ºC).
Brewing time: perhaps 1 hour. Most of the hydrogen gas is produced in the first 30 minutes or so, and then the reaction starts to slow down; once the reaction looks like it has almost stopped, then it is brewed. You could even shorten the brew time to say 40 minutes if you are in a rush.
But it is crucial to vigorously shake the bottle for 30 sec at the end of the brewing time. If you don't shake vigorously, you will end up with a weak 1 ppm hydrogen rich water rather than a strong 5 ppm. It is the 30 seconds of shaking that helps dissolve much of the H2 gas into the water.
Bottle capacity: as you like it; anything from a 500 ml plastic Coke bottle or similar soda bottles, to a large 2 liter soda bottle. Always fill the bottle to the very top with water. I typically use a 1.5 liter bottle that held sparkling mineral water. Obviously you cannot use bottles that hold non-sparkling drinks, as these are not designed to withstand pressure.
There is plenty of hydrogen gas made in the reaction, so you should have enough to cover even for 2 liters of water (although if you are using a 2 liter bottle, perhaps put in slightly more citric acid, say 4 grams).
Though there's not much point in using very large bottles, because hydrogen rich water has a half life of around 2 hours once the bottle is opened and the pressure released (reference: see the MHF website). So you have to drink it fresh. But larger bottles are good if you want to share it with other members of your household each time you brew; in which case, perhaps figure for each person drinking a dose of 250 to 500 ml of hydrogen rich water (just as a guideline).
How did you measure the H2 amount released in a home setting?
I guess the ppm calculation is based on the 1.57 x (pressure = occupied volume / the amount above).
Not quite: the 1.57 figure relates to Henry's Law; but to calculate pressure we use Boyle's Law.
I'll explain the bottle internal pressure measurement and calculation step by step:
Firstly, you measure the volume occupied by the pressurized H2 in the bottle, after it has brewed for and hour or two. The H2 gas collects in the top 5 cm or so of the bottle, so by marking on the bottle where the waterline is (which will be around 5 cm down from the bottle cap), when you later empty the bottle, you can work out how much volume is in the space above the marked waterline just by placing a small amount of water into the bottle, and with the bottle cap closed and the bottle inverted, adjusting the amount of water in the bottle until the water surface lines up with the marked waterline. Then that volume of water is exactly equal to the volume of pressurized H2 gas that was in the bottle. It's hard to describe, but easy to do.
(Note that if there is very high pressure inside the bottle (say > 6 or 7 atmospheres), so that the bottle is ballooned out under pressure, then this method becomes slightly inaccurate, although I figured out how to compensate for this inaccuracy.)
Secondly, to measure the volume of the H2 gas when it escapes from the bottle at normal atmospheric pressure, you simply open the cap of the pressurized bottle under water, with a large upturned container (like a large one pint beer glass) filled up with water placed just above the bottle cap. Then as you open the cap, the pressurized H2 gas that escapes collects in the upturned container, displacing the water in the container downwards.
Once you have collected all the escaped H2 gas in this way, you mark the H2 gas waterline on this upturned container. Then you place your container back upright, fill with water up to the marked waterline, and then measure the volume of that water. That gives you the total volume of H2 gas that has escaped from the bottle, that is to say, the volume of the H2 gas when it is at normal atmospheric pressure.
Note that 1 ml of water weighs 1 gram, so you can use a gram weighing scales to measure water volume.
Finally, you calculate the ratio of these two volumes, and that gives you the internal pressure in the bottle:
Pressure inside the bottle in atmospheres =
volume of the H2 gas at normal atmospheric pressure / volume of the H2 gas when pressurized inside the bottle
This calculation is based on Boyle's law.
Edited by Hip, 06 November 2016 - 06:31 PM.